The expected value is the sum of the products of the probability of each outcome and the payout for that outcome:
Probability of winning:
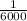
Payout for winning:
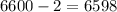
Probability of not winning:
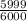
Payout for not winning:
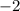
Therefore:
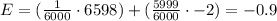
Answer:
The expected value of a single ticket is -$0.9