Question

An architect designs two similar triangular patios. The first has angle measures of (x-7), (y+10), and 84. The second patio has angle measures of (x+30), 47, and 49. Find the value of x and y.

Answer 1

Since the sum of angles of a triangle is 180 degrees

Since the measures of the 3 angles of the 1st triangle are

`(x-7)^(\circ),(y+10)^(\circ),84^(\circ)`

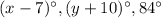
Add them and equate the sum by 180 degrees

`x-7+y+10+84=180`

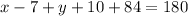
Add the like terms on the left side

`\begin{gathered} x+y+(-7+10+84)=180 \\ x+y+87=180 \end{gathered}`

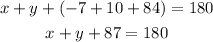
Subtract 87 from both sides

`\begin{gathered} x+y+87-87=180-87 \\ x+y=93\rightarrow(1) \end{gathered}`

Since the measures of the 3 angles of the other triangles are

`(x+30)^(\circ),47^(\circ),49^(\circ)`

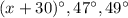
Add them and equate the sum by 180 degrees

`x+30+47+49=180`

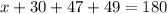
Add the like terms on the left side

`\begin{gathered} x+(30+47+49)=180 \\ x+126=180 \end{gathered}`

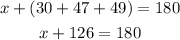
Subtract 126 from both sides

`\begin{gathered} x+126-126=180-126 \\ x=54 \end{gathered}`

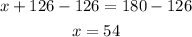
Substitute the value of x in equation (1) to find y

`54+y=93`

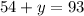
Subtract 54 from both sides

`\begin{gathered} 54-54+y=93-54 \\ y=39 \end{gathered}`

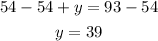
The answers are:

x = 54

y = 39