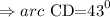Answer:
The part A can be calculate using the secant theorem below
To figure out the value of triangle ADB, we will use the formula below
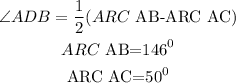
By substituing the values, we will have
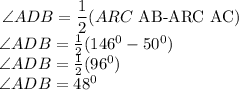
Hence,
The value of angle ADB is
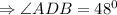
Part B:
To figure out the value of arc angle CD, we will use the formula below
Hence,
The formula will be
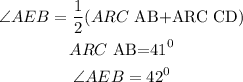
By substituting the values, we will have
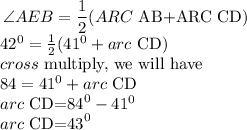
Hence,
The value of arc CD is