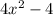Solution:
In your own words, describe two binomials that, when multiplied, results in the difference of two squares.
Let the binomials be
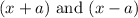
Where the first term is x and the second term is a
Multiplying the binomials
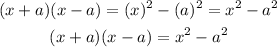
Hence, when multiplied, the result is the difference of two squares.
Assuming the binomials, for example are
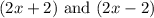
Their product will give
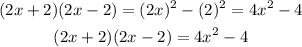
Hence, the product is