Question

In the Triangle below the length of AC is 6 what is the length of BC

Answer 1

Right triangles

Initial explanation

We know that the tangent equation if given by:

`\tan (\alpha)=\frac{opposite\text{ side}}{\text{adjacent side}}`

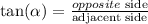
In this case, with respect to 30º, the opposite side is AC and the adjacent is BC:

Tangent equation in this case

Then, in this case, we have

`\begin{gathered} \tan (30º)=\frac{AC}{\text{BC}} \\ \\ \end{gathered}`

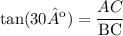
since tan(30º) = 0.577 and AC = 6, then:

`\begin{gathered} \tan (30º)=\frac{AC}{\text{BC}} \\ \downarrow \\ 0.577=\frac{6}{\text{BC}} \end{gathered}`

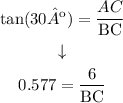
Finding BC

Now, we can solve the equation for BC "leaving it alone".

Step 1- taking BC to the left side, we have:

`\begin{gathered} 0.577=\frac{6}{\text{BC}} \\ \downarrow \\ 0.577\cdot BC=6 \end{gathered}`

Step 2- taking 0.577 to the right side:

`\begin{gathered} 0.577\cdot BC=6 \\ \downarrow \\ BC=(6)/(0.577) \end{gathered}`

Then,

`BC=(6)/(0.577)\cong10.4`

Answer: BC = 10.4