Question

y6What is the equation of the line parallel to the given linewith an x-intercept of 4?y =421X5-4-332-345

Answer 1

`y=4x-16`

Step-by-step explanation

We want to find the equation of the line that is parallel to the given line.

A line that is parallel to a given line will have the same slope as the line.

Therefore, we first have to find the slope of the given line.

To find the slope, we apply the formula for slope:

`m=(y_2-y_1)/(x_2-x_1)`

where (x1, y1) and (x2, y2) are two points that pass through the given line.

Let us pick points (-3, -3) and (-1, 5)

The slope is:

`\begin{gathered} m=(5-(-3))/(-1-(-3))=(5+3)/(-1+3) \\ m=(8)/(2) \\ m=4 \end{gathered}`

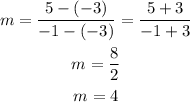
The slope is 4.

The general form of a linear equation is given as:

`\begin{gathered} y=mx+b \\ m=\text{slope} \\ b=y\text{ intercept} \end{gathered}`

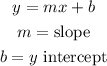
We are given the x intercept.

The x intercept is the value of x when y is 0.

This means that we can find b in the equation if we substitute the slope and the x intercept of the equation.

That is:

`\begin{gathered} 0=4(4)+b \\ \Rightarrow0=16+b \\ \Rightarrow b=-16 \end{gathered}`

Therefore, the equation of the line parallel to the given line is:

`y=4x-16`