We are asked to determine the velocity of a bicycle when a force of 346 N is applied to it. To do that we will use a balance of energy.
The work applied to the bike is equivalent to the change in kinetic energy of the bicycle. Therefore, we have:
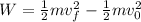
since the bicycle starts from rest this means that the initial velocity is zero:
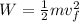
Since work is the product of force by distance we have:
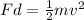
Where "F" is the force and "d" is the distance.
Now, we solve for the velocity. To do that we will multiply both sides by 2:
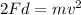
Now, we divide both sides by the mass:
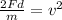
Now, we take the square root to both sides:
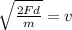
Now, we substitute the values:

Solving the operations:
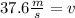
Therefore, the velocity is 37.6 meters per second.