Question

Find the critical numbers of the function f(x) = 12x ^ 5 + 15x ^ 4 - 80x ^ 3 - 5 and classify them using a graph

Answer 1

The function is given to be:

`f\left(x\right)=12x^5+15x^4-80x^3-5`

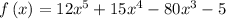
The graph of the function is shown below:

The critical points are points where the function is defined and its derivative is zero or undefined.

The derivative is calculated to be:

`f^(\prime)(x)=60x^4+60x^3-240x^2`

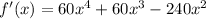
The critical points are at f'(x) = 0:

`\begin{gathered} 60x^4+60x^3-240x^2=0 \\ Simplifying \\ x^4+x^3-4x^2=0 \end{gathered}`

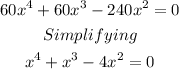
Factoring:

`x^2(x^2+x-4)=0`

Therefore, applying the zero factor principle:

`\begin{gathered} x^2=0 \\ \therefore \\ x=0 \end{gathered}`

or

`\begin{gathered} x^2+x-4=0 \\ Using\text{ }the\text{ }Quadratic\text{ }Formula \\ x=1.56155,x=-2.56155 \end{gathered}`

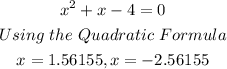
Therefore, the critical numbers are given below with their descriptions:

`\begin{gathered} x=-2.56155,\text{ Local Maximum} \\ x=0,\text{ Neither a maximum or a minimum} \\ x=1.56155,\text{ Local Minimum} \end{gathered}`