Question

use the graph below and synthetic division to identify all zero sand their characteristics of the function

Answer 1

Answer:

x = -3, multiplicity = 1 odd

x = -1, multiplicity = 2, even

x = 1, multiplicity = 2, even

Explanations:

The given polynomial is:

`x^5+3x^4-2x^3-6x^2+x+3`

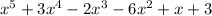
The zeros of a graph can be determined as the point where the y-value is zero

By careful observation of the graph:

The values of x at which y = 0 are:

x = -1, x = 1, and x = -3

To Identify the multiplicities of the zeros:

Note that

every value of x that crosses the x axis has a odd multiplicity

every value of x that bounces back when it touches the x-axis has an even multiplicity

Therefore:

x = -3 has a odd multiplicity ( 1 time)

x = -1 has an even multiplicity (2 times)

x = 1 has an even multiplicity (2 times)