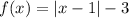Remember the following transformation rules for functions:
Vertical translation up c units:
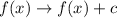
Vertical translation down c units:
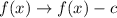
Horizontal translation left c units:
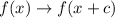
Horizontal translation right c units:
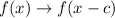
If the given function, f(x)=|x| must be shifted down 3 units and to the right 1 unit, then, substract 3 from the function and substract 1 from the argument of the function.
First, perform a vertical translation down 3 units:
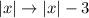
Next, perform a horizontal translation right 1 unit:
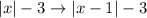
Therefore, the new equation is: