Let's call one of the numbers as x and the other as y.
From the first sentence
"One number is 9 more than 3 times another."
From this sentence, we know that our first number(x) plus 9 is equal to 3 times the other(y).
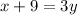
From the other sentence
"Their product is 9 more than 3 times their sum"
We get the following equation

Now we have two equations for two variables
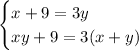
Expanding the parentheses, we have
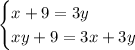
Using our value for 3y in the first equation in the second equation, we get a new equation
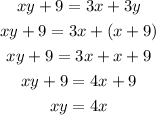
This last equation have an immediate solution, x = 0. If x is not 0, we can divide both sides by x.

Using this value for y, we can evaluate any of the equations to find its corresponding x, and we can do the same for x = 0 to find the corresponding value for y.

This means, our points are (0, 3) and (3, 4).