Answer:
• Width: 9 m
,
• Length: 27 m.
Explanation:
Let the width of the alley = w.
The length of the alley is three times the width, therefore:
• The length of the alley = 3w
The perimeter of the alley = 72 m.
The perimeter of a rectangle is calculated using the formula:
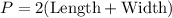
Substitute the values:
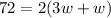
Solve the equation for w.
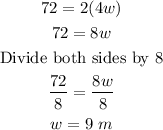
Finally, find the length of the alley.

The width is 9 m and the length is 27 m.