Question

The answer options are the 4 options given for all the answers, all of those options contain the right answer for part of the problem but need to be put in their correct place.

Answer 1

Part A. When we have two chords that intercept at one of the exterme points of a circle, like this:

Then the relationship between the minor arc and the interior angle of the chords is:

`y=(1)/(2)x`

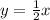
therefore, if we substitute according to the given circle we have:

`a=(150)/(2)=75`

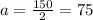
Therefore, angle a is 85°.

Part B. The angle formed by a tangent and a chord of a circle is half the the arc that is formed:

We have that:

`y=(1)/(2)x`

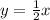
Now, we substitute:

`b=(1)/(2)(210)=105`

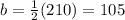
Therefore, "b" is 105°.

Part C. Given the following configuration:

The following relationship holds:

`ab=cd`

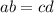
Now, we substitute the values according to the given circle:

`(13)(c)=(16)(11)`

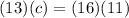
Now, we divide both sides by "c":

`c=((16)(11))/((13))=13.5`

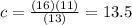
Therefore, the value of "c" is 13.5

Part D. In the following configuration:

The following relationship holds:

`x=(1)/(2)(x+z)`

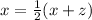
Now, we substitute the values:

`d=(1)/(2)(85+75)`

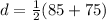
Solving the operations:

`d=80`

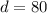
therefore, the angle "d" is 80 degrees.