Question

5. A function fis given by f(x) = 4x3 + - 3,x+ 0.(a) Write down the derivative off.(b) Find the point on the graph off at which the gradient of the tangent is equal to 6.

Answer 1

a. The derivative is :

`f^(\prime)(x)=12x^(2)-(6)/(x^(3))`

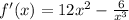
b. The point on the graph is (1, 4)

EXPLANATION :

From the problem, we have the function :

`f(x)=4x^3+(3)/(x^2)-3`

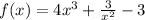
a. The derivative will be :

`\begin{gathered} f^(\prime)(x)=3(4x^2)+(-2)((3)/(x^3)) \\ f^(\prime)(x)=12x^2-(6)/(x^3) \end{gathered}`

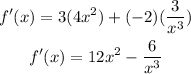
b. The gradient of the tangent is also the derivative which is f'(x)

So we need to find the point in which f'(x) = 6

That will be :

`\begin{gathered} 6=12x^2-(6)/(x^3) \\ \text{ Multiply both sides by x\textasciicircum3} \\ 6x^3=12x^5-6 \\ \text{ Divide both sides by 6} \\ x^3=2x^5-1 \\ x^3-2x^5=-1 \\ 2x^5-x^3=1 \\ x^3(2x^2-1)=1 \end{gathered}`

Equate both factors to 1 :

`\begin{gathered} x^3=1 \\ x=1 \\ \\ 2x^2-1=1 \\ 2x^2=2 \\ x^2=1 \\ x=1 \end{gathered}`

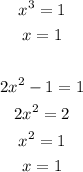
So we have x = 1

Substitute x = 1 to the original function :

`\begin{gathered} f(1)=4(1)^3+(3)/((1)^2)-3 \\ f(1)=4+3-3 \\ f(1)=4 \end{gathered}`

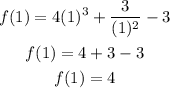
Therefore the point is (1, 4)