We are given the following right triangle:
We are asked to determine segment AI. To do that we can apply the Pythagorean theorem which states:
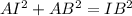
Now we solve for AI, first by subtracting AB squared from both sides:
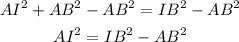
Now we take the square root to both sides:
![AI=\sqrt[]{IB^2-AB^2}](https://img.qammunity.org/2023/formulas/mathematics/college/r49cdgeqz90sxftywfosqcinf44fhkvenu.png)
Now we replace the given values:
![AI=\sqrt[]{(500ft)^2-(300ft)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/kn1cys9fyujlelwssgqxr1zqoz53lgtkfc.png)
Solving the operations:
![AI=\sqrt[]{250000ft^2-90000ft^2}](https://img.qammunity.org/2023/formulas/mathematics/college/dnuciakiq35jl2gagy0wpq1wcrm7i9y7dt.png)
Solving the subtraction:
![AI=\sqrt[]{160000ft^2}](https://img.qammunity.org/2023/formulas/mathematics/college/t0gqpt0d7ps9p6cfhllsb46imoonglfwnt.png)
Solving the square root:
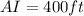
Therefore, the distance AI is 400 feet.
Now, we have the following triangle:
We can also use the Pythagorean theorem in this triangle:
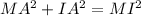
To solve for the distance MI we will take the square root to both sides:
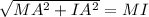
Now we replace the values:
![\sqrt[]{(100ft^{})^2+(400ft)^2}=MI](https://img.qammunity.org/2023/formulas/mathematics/college/lrqcue2kitkvr3lm13q9bh14pe4vkxqw5s.png)
Solving the operations we get:
![\sqrt[]{170000ft^2}=MI](https://img.qammunity.org/2023/formulas/mathematics/college/5ak27wta9efkr40kw39ez2yj9u84lkee9c.png)
Now we solve the square root:
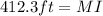
Therefore, the distance MI is 412.3 feet.
Now we are asked to calculate the angle I. To do that we will use the trigonometric function tangent since this function is defined as:

Replacing the values:
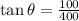
Simplifying:
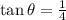
Now we take the inverse function of tangent:
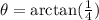
Solving the operation we get:
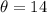
Therefore the angle is 14 degrees. The angle at the launching point is angle M, since we have a right triangle this angle must be equal to:

Therefore, in compliance with regulations.