Question

Find the sum of the first 16 terms in an arithmetic series where a1=2, and the common difference is d=2A)306B)240C)272D)360

Answer 1

This problem is about arithmetic sequence sums, which can be defined by the following formula-

`S_n=(n)/(2)(2a_1+(n-1)d)`

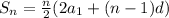
Where d refers to the difference, and a1 refers to the first term. We know by given that d=2 and a1=2. Additionally, n refers to the total numbers of terms which are 16.

Knowing all these variables, we use the formula

`S_(16)=(16)/(2)(2(2)+(16-1)2)=8(4+30)=8(34)=272`

As you can observe, the sum of all 16 terms is 272.

Therefore, the right answer is 272.