Question

If Terri swam 3 laps in 2.5 minutes, how long would it take her to swim 20 laps at the same rate?

Answer 1

Given:

a.) Terri swam 3 laps in 2.5 minutes.

To be able to determine how long would it take her to swim 20 laps, we will be using ratio and proportions.

`\text{ 3 laps : 2.5 minutes = 20 laps : x}`

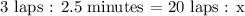
Where,

x = time to swim 20 laps

We get,

`\text{ 3 laps : 2.5 minutes = 20 laps : x}`
`\text{ }\frac{\text{ 3 laps}}{\text{ 2.5 mins.}}=\text{ }\frac{\text{ 20 laps}}{\text{ x}}\text{ }\rightarrow\text{ }\frac{\text{ 3}}{\text{ 2.5}}\text{ = }\frac{\text{ 20}}{\text{ x}}`
`\text{ (3)(x) = (20)}(2.5)`
`\text{ 3x = 50}`
`\text{ }\frac{\text{3x}}{3}\text{ = }\frac{\text{50}}{3}`
`\text{ x = 16.6666}\ldots\text{ }\approx\text{ 16.67 or 16 }(2)/(3)\text{ minutes}`

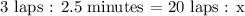
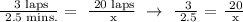
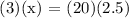
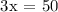
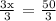
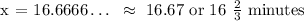
Therefore, Terri will take 16.67 or 16 2/3 minutes to swim 20 laps/