Question

asic Geometric Shapes - Part 1 What is the value of x (3x +50) Enter your answer in the box. (6x - 10)

Answer 1

1) From the picture, we see that we have two vertical angles:

`\begin{gathered} A=(3x+50)^(\circ) \\ B=(6x-10)^(\circ) \end{gathered}`

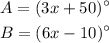
2) Now, because of the "Vertical Angles Postulate" from geometry, we know that angles A and B are equal, so equalling the angles and replacing by their expression from above, we get the following equation in terms of x:

`\begin{gathered} A=B \\ 3x+50=6x-10 \end{gathered}`

3) We must solve the last equation for x, doing that we find:

`\begin{gathered} 3x+50=6x-10 \\ 50=6x-10-3x \\ 50+10=6x-3x \\ 60=3x \\ x=(60)/(3) \\ x=20 \end{gathered}`

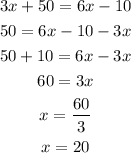
Steps to solve the equation

0) We have the equation:

`3x+50=6x-10`

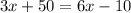
1) We want all the terms with x on one side, and the other on the other one. So we pass the term +3x to the right as -3x:

`50=6x-10-3x`

2) Now we pass the term -10 to the left as +10:

`50+10=6x-3x`

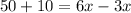
3) We sum the terms on each side:

`60=3x`

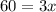
4) We pass the 3 that multiplies the x on the right, dividing the 60 on the left:

`x=(60)/(3)`

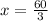
5) Finally we make the division and we get:

`x=20`

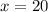
Answer

x = 20