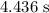Question

A motorcycle traveling along a straight road increases its speed from 28.1 ft/s to 53.5ft/s in a distance of 181 feet. If the acceleration is constant, how many seconds of timeelapses while the motorcycle moves this distance?

Answer 1

Given Data:

*The initial speed of the motorcycle is:

`u=28.1\text{ ft/s}`

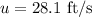
*The final speed of the motorcycle is:

`v=53.5\text{ ft/s}`

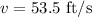
*The distance is:

`s=181\text{ ft}`

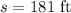
Step-by-step explanation:

Using the third kinematics equation of motion, we get:

`2as=v^2-u^2`

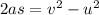
Substituting the known values, we get:

`\begin{gathered} (53.5\text{ ft/s})^2-(28.1\text{ ft/s})^2=2a(181\text{ ft}) \\ 2862.25\text{ ft}^2\text{/s}^2-789.61\text{ ft}^2\text{/s}^2=a(362\text{ ft}) \\ 2072.64\text{ ft}^2\text{/s}^2=a(362\text{ ft}) \\ a=\frac{2072.64\text{ ft}^2\text{/s}^2}{362\text{ ft}} \\ a=5.726\text{ ft/s}^2 \end{gathered}`

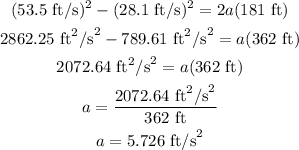
Using the first kinematics equation, we get:

`v=u+at`

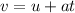
Substituting the known values, we get:

`\begin{gathered} 53.5\text{ ft/s = 28.1 ft/s +\lparen5.726 ft/s}^2\text{\rparen t} \\ 25.4\text{ ft/s = \lparen5.726 ft/s}^2)t \\ t=\frac{25.4\text{ ft/s}}{\text{5.726 ft/s}^2} \\ t=4.436\text{ s} \end{gathered}`

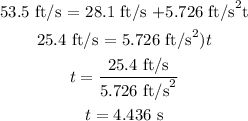
Final Answer:

The time elapsed while the motorcycle moves this distance is:

`4.436\text{ s}`