Question

Topic 5: Solving Proportional word problems.Note: A proportion is an equation that states that two ratios are equivalent. Todetermine whether a pair of ratios forms a proportion, use cross products. You canalso use cross-products to solve proportions.Ex 5: solve each using a proportion.a.6 cans of soup cost $2.46.How much would 10 cans cost?b. If ½ h lb of turkey has 320 calories,how many calories are in 3/4 pounds?

Answer 1

To apply cross-products to solve proportion you have to multiply opposite numerators and denominators together.

Then, let's start with a.:

a. 6 cans of soup cost $2.46. How much would 10 cans cost?

Let's form the ratios:

`\frac{6\text{ cans}}{2.46\text{ \$}}=\frac{10\text{ cans}}{x\text{ cost}}`

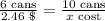
If you use cross-products you will obtain:

`\begin{gathered} 6* x=10*2.46 \\ \text{Divide both sides by 6} \\ (6* x)/(6)=(10*2.46)/(6) \\ \text{Simplify} \\ x=(10*2.46)/(6)=4.1 \end{gathered}`

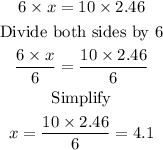
Thus, 10 cans would cost $4.1.

b. If ½ h lb of turkey has 320 calories, how many calories are in 3/4 pounds?

The ratios are:

`\begin{gathered} \frac{1/2\text{ lb}}{320\text{ calories}}=\frac{3/4\text{ lb}}{x} \\ \text{Multiply both sides by 320} \\ \frac{1/2\text{ lb}}{320\text{ calories}}*320calories=\frac{3/4\text{ lb}}{x}*320calories \\ \text{Simplify} \\ 1/2\text{ lb}=\frac{3/4\text{ lbx 320 calories}}{x} \\ \text{Multiply both sides by x} \\ 1/2\text{ lb}* x=\frac{3/4\text{ lbx 320 calories}}{x}* x \\ \text{Simplify} \\ 1/2\text{ lb}* x=3/4*320\text{ calories} \\ \text{Divide both sides by 1/2} \\ \frac{1/2\text{ lb}* x}{1/2\text{ lb}}=\frac{3/4lb*320\text{ calories}}{1/2\text{ lb}} \\ \text{Simplify} \\ x=\frac{3/4lb*320\text{ calories}}{1/2\text{ lb}}=480\text{ calories} \end{gathered}`

Thus, 3/4 pounds have 480 calories.