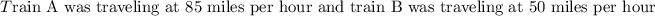Given:
Train A has a speed of 35 miles per hour greater than that of train B.
If train A travels 340 miles at the same time train B travels 200 miles.
Required:
We need to find the speed of each train.
Step-by-step explanation:
Let x miles per hour be the speed of train B.
The speed of train A is 35 miles per hour greater than x miles per hour.
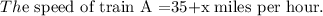
The distance of train A is 340 miles.
Consider the speed formula.
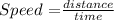
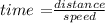
Substitute distance =340 miles and speed = 35+x in the formula to find the time taken by train A to travel 350 miles.
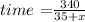
The distance of train B is 200 miles.
Substitute distance = 200 miles and speed =x in the formula to find the time taken by train B to travel 200 miles.
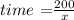
Train A and B take the same time to travel 350 miles and 200 miles respectively.
Equate both equations of the time.
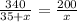
Use the cross-product method.
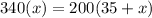
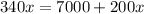
Subtract 200x from both sides of the equation.
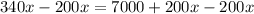
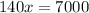
Divide both sides of the equation by 140.
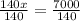
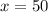
We get that the speed of train B is 50 miles per hour.
Substitute x =50 in the speed of train A =35+x miles per hour.
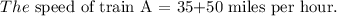
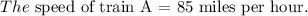
Final answer: