Question

Find the x-intercept and y-intercept of the line.6x – 4y= 21-Write your answers as exact values. Do not write your answers as ordered pairs.x-intercept: y-intercept:

Answer 1

The x-intercept, is the x-value when the function "cuts" the x-axis, when y = 0. To find the x-intercept we just need to evaluate the function at y = 0.

`\begin{gathered} 6x-4\cdot0=21 \\ \Rightarrow x=(21)/(6)=(7)/(3) \end{gathered}`

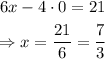
The y-intercept follows the same idea, then, we just need to evaluate the function at x = 0.

`6\cdot0-4y=21\Rightarrow y=-(21)/(4)`

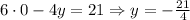
Then, our intercepts are:

`\begin{gathered} x-\text{intercept}=(7)/(3) \\ y-\text{intercept}=-(21)/(4) \end{gathered}`