Question

Find the Value of X in simplest radical form and Find the measure of angle A.​

Answer 1

A = 30°

x = 9·√3

Explanation:

Part A

In the drawing, we are given;

The radius of the circle with center at point S = SA = 18

ΔAHA is a right triangle

One of the leg length of ΔASH = 9

The length of the hypotenuse side of ΔASH, AS = 18 The radius of the circle with center at the point 'S'

By Pythagoras's theorem, the length of the (radius) side, AS = √(SH² + AH²)

∴ AH = √(AS² - SH²)

AH = √(18² - 9²) = √(243) = 9·√3

AH = 9·√3

By circle theorem, SH bisects the line AH extended to the circumference of the circle

SH bisects the line with length AH + x

∴ AH = x

x = AH = 9·√3

x = 9·√3

Part B

By trigonometric ratios, we have;

`sin\angle A = (Opposite \ leg \ length)/(Hypotenuse \ length)`

`\therefore sin\angle A = (9)/(18) = (1)/(2)`

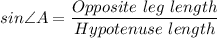
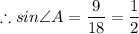
∠A = arcsine (1/2) = 30°

Angle A = 30°