Okay, here we have this:
Considering the provided equation system, we are going to solve it, so we obtain the following:

We will start by clearing for x for the first equation:
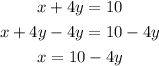
Now, we are going to replace "x" with this in the second equation:
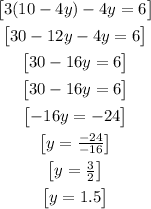
And, finally we are going to replace "y" with 1.5 in the equation that we found for x:
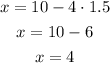
Finally we obtain that solution of the system is (4, 1.5).