Question

Pic provided with question A) B ) growth/decay rate is____C) continuous growth/decay rate is____

Answer 1

Given:

`y=f(t)=31(1.02)^t`

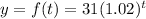
A) We are to write the exponential function in the form

`y=ae^(kt)`

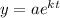
When t = 1

`f(1)=31(1.02)^1=31(1.02)`

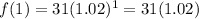
Also,

`f(1)=ae^(k(1))=ae^k`

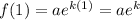
Equating the two equations and solving for k

`\begin{gathered} 31(1.02)=ae^k \\ \therefore a=31 \\ We\text{ then have,} \\ 1.02=e^k \end{gathered}`

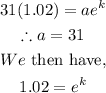
Apply exponent rules:

`\begin{gathered} k=\ln \mleft(1.02\mright)=0.01980\approx0.0198(4\text{ decimal places)} \\ \therefore k=0.0198 \end{gathered}`

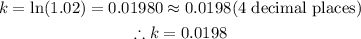
B) The annual growth rate is,

`\begin{gathered} y=ab^x \\ \text{where,} \\ b=1+r=1.02 \end{gathered}`

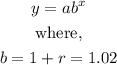
Equating the two expressions together and solving for r

`\begin{gathered} 1+r=1+0.02 \\ r=1+0.02-1=1-1+0.02=0.02=2\% \\ \therefore r=2\% \end{gathered}`

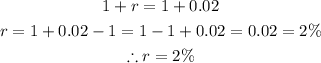
Hence, the annual growth rate is 2% per year.

C) The continuous growth rate is the constant k which is

`\begin{gathered} k=0.0198=1.98\% \\ \therefore k=1.98\% \end{gathered}`

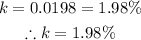
Hence, the continuous growth rate is 1.98% per year.