Question

On the whiteboard draw a right triangle and prove thePythagorean Theorem using similar triangles.

Answer 1

In the development of the step by step, you will find the detailed answer

Explanation:

We have the following triangle, which is made up of two other triangles:

If the triangle ABC is right, then:

`\begin{gathered} (AC)^2+(CB)^2=(AB)^2 \\ or \\ b^2+a^2=c^2 \end{gathered}`

The triangle ABC and the triangle DBC by the similar triangles theorem, which says:

If the height corresponding to the hypotenuse is plotted in a right triangle, the two triangles formed are similar to each other, and similar to the given triangle.

Therefore:

`\begin{gathered} (c)/(a)=(a)/(n)\rightarrow cn=a^2 \\ (c)/(b)=(b)/(m)\rightarrow cm=n^2 \end{gathered}`

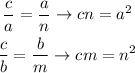
If we add we would be:

`\begin{gathered} cn+cm=a^2+b^2 \\ c(n+m)=a^2+b^2 \\ n+m=c \\ \text{ therefore} \\ c\cdot c=a^2+b^2 \\ c^2=a^2+b^2 \end{gathered}`

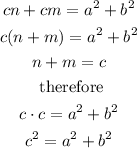
In this way, using the similarity between the triangles ABC and DBC, we arrive at what is the Pythagorean theorem.