To determine which tables have equivalent ratios, the first step is to determine the rate of change (k) of each relationship shown in each table.
To determine the rate of change you have to select any ordered pair of the table and divide the value corresponding to the y-coordinate by the value corresponding to the x-coordinate:
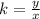
Table a
The variable "hours" is the independent variable "x" and the variable "Pay in dollars" is the dependent variable "y", to determine the rate of change of this relationship you can use, for example, the ordered pair (7,52), so that:
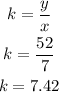
Choose another ordered pair, for example (5,40)
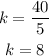
The rates of change of the relationship are not constant.
Table b
The variable "blue" will be the independent variable "x" and the variable "yellow" will be the dependent variable "y"
To determine the rate of change choose one ordered pair, for example, (4,8)
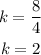
If you choose another ordered pair of this table, for example (10,16), the rate of change obtained will be:
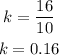
This table doesn't show constant rates of change, the relationship shown is not linear.
Table c
At a glance, you can see that the ordered pairs shown on the table are almost the same as "a"
Choose an ordered pair and calculate the rate of change (7,56)
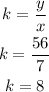
Choose another pair, for example, (3,24)
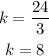
This table has an equivalent change of rate.
The correct option is table c.