An hemispherical dome is half a sphere. If the diameter is 60 m, then the radius is 30 m.
We can use differentials to solve this problem because we are adding a thin layer to the original dome, so the volume of the dome in increased by a differential of itself.
This differential volume that the dome is increased is equal to the volume of the coat of paint.
The volume of the dome can be written as:
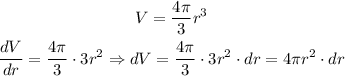
Now, we can calculate dV as:
![\begin{gathered} dV=4\pi r^2\cdot dr \\ dV\approx4\cdot3.14\cdot(30m)^2\cdot0.07\operatorname{cm}\cdot\frac{1m}{100\operatorname{cm}} \\ dV\approx12.57\cdot900m^2\cdot0.0007m \\ dV\approx7.92m^3 \end{gathered}]()
Answer: the paint needed for this coat is approximately 7.92 m^3