Question

graph a right triangle with two points forming the hypotenuse. using the sides, find the distance between the two points, to the nearest tenth if possible (6,-5) and (-3, 3)

Answer 1

We will have the following:

*First. We determine a new point that can be used to complete the rigth triangle; we are given the points:

`\begin{cases}(6,-5) \\ \\ (-3,3)\end{cases}`

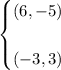
So, a point we could use to form a rigth triangle could be:

`(-3,-5)`

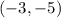
And we would have the following triangle:

*Second: We determine the distances:

**Distance on the horizontal axis would be 9 units.

**Distance on the vertical axis would be 8 units.

*Third: We determine the distance betweem the two original points:

`h=\sqrt[]{9^2+8^2}\Rightarrow h=\sqrt[]{145}`
`\Rightarrow h=12.04159458\ldots\Rightarrow h\approx12`

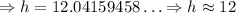
So, the distance between the two original points is approximately 12 units.