A standard deviation as the term implies is the measure of how much data deviates (moves away from) from the mean of the data set. If the mean for example is calculated as 13, then the standard deviation would show you how far the data set is from 13. If they are quite far then the standrad deviation is high, and if they are quite near then the standard deviation is low.
We can now inspect the data provided for set A and set B.
For set A, by inspection we can see that the numbers;
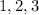
are quite far from the average, which is 13.
Similarly, the numbers;
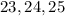
are also quite far from the average of 13. Hence. set A has a high Standard Deviation.
For set B, which has the same average of 13, the numbers;
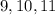
are closer to the avearge 13 (when compared to 1,2 and 3).
The same can be said of numbers;

These too are closer to the average (when compared to 23, 24 and 25).
The conclusion is that set A has a larger SD. The numbers are farther from the average, that is
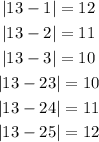
For set B, the the SD is smaller. The numbers are clustered closer to the average, that is;
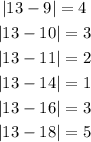
For set A, the numbers deviate as far away as 12 units.
For set B, the numbers deviate but not as far away as set A
ANSWER:
Option A is the correct answer