Given:
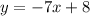
Let's find the values of x where the tangent line to the graph of f(x) is parallel to the given line.
Where:
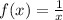
Let's first find the derivative of f(x).
We have:
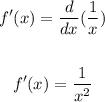
Apply the slope-intercept form:
y = mx + b
Where m is the slope.
Now, from the equation:
y = -7x + 8
The slope of the line is -7.
Now if the tangent of f(x) =1/x is parallel to the line, f'(x) will be the slope of the line.
Thus, we have:
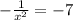
Now, let's solve for the values of x.
Multiply both sides by x²:
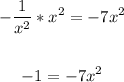
Divide both sides by -7:
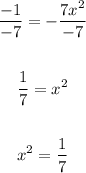
Take the square root of both sides:
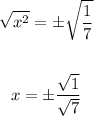
Solving further:
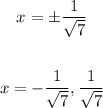
Therefore, we have the following:
• The greater solution is x = 1/sqrt(7)
,
• The lesser solution is x = -1/sqrt(7).
ANSWER:
• The greater solution is x = 1/sqrt(7)
,
• The lesser solution is x = -1/sqrt(7).