Let X denote the number of claims. If X has a Poisson distribution, then, based on the given information you can write:
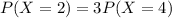
Then, by using the Poisson distribution:
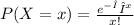
you can write:
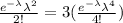
Now, it is neccesary to determine the solution for λ from the previous equation. Cancel e^-λ both sides, divide by λ^2 both sides and the apply square root and solve for λ:
![\begin{gathered} (λ^2)/(2)=3(λ^4)/(24) \\ λ^2=4 \\ λ=\sqrt[\placeholder{⬚}]{4}=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1joxw4zrv0wh0sw6n838voqw9k6u3iiytr.png)
Now, consider that the variance in a Poisson distribution is given by
σ^2 = λ
Hence, the variance of the number of claims filed is 2