'Ten minus a number' this translates as:

'is greater than or equal to 21'. This means that the expression above is > or = to 21:
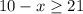
To solve it we have to do the same operations in both sides of the inequality.
First we add x in both sides. This way, we'll get possitive x on the right side:
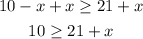
And finally we substract 21 on both sides:
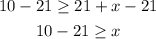
And finally we compute the substraction. The solution of the inequality is:
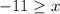
That can also be writen as:
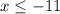
Is the same expression written backwards, it's easier to read.