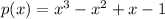Polynomials
A polynomial can be built if we know its zeros, also called roots
Suppose p,q, and r are the roots of a polynomial of degree 3, then:
p(x)=a(x-p)(x-q)(x-r)
Where a is a real number different from 0
Note we are only given two roots:
p=1
q=i
recall that i is the base of the complex numbers, that is:
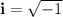
The third root comes when we recall that, if a polynomial has real coefficients, the complex roots come in conjugate pairs, i.e. if a+bi is one root of the polynomial, then a-bi is also a root of the polynomial.
Thus, the other root is the conjugate of q:
r=-i
Now we have all the roots, we just apply the above equation to find:
p(x)=a(x-p)(x-q)(x-r)
p(x)=a(x-1)(x-i)(x+i)
Recall that
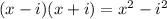
Since
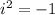
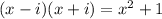
Finally, the required polynomial is:
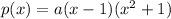
Since no other condition is given, we choose a=1:

This is the required polynomial
Operating the products:

Ordering: