From the graph, the dotted lines represent the average salaries of Baseball players, while the other line represent the average salaries of the basketball players.
Let's solve for the following.
• (1) Estimate the year that the salaries were equal and estimate the salaries.
The point where the salaries were equal will be the point where both lines meet. It is the solution to the set of lines which is also called the point of intersection.
Looking at the graph, we can see the lines meet at the point:
(x, y) ==> (5, 300)
Thus, the year is at year 5.
1980 + 5 = 1985
Therefore, the year where the salaries were equal is in 1985.
The estimated salary at year 5 was $300 thousand.
• (2). ,Estimate the y-intercept of each line.
The y-intercept is the point the line crosses the y-axis.
Thus, we have:
Estimated y-intercept for Basketball ==> y = 90
Estimated y-intercept for baseball ==> y = 150.
Let's find the equation of each line using the point of intersection and y-intercept.
Where:
Point of intersection: (5, 300)
APply the slope intercept form:
y = mx + b
Where m is the slope and b is the y-intercept.
Thus, we have:
Equation for Basketball.
We have the points:
(x1, y1) ==> (0, 90)
(x2, y2) ==> (5, 300)
Find the slope using the slope formula:
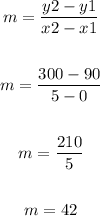
The slope of basketball line is = 42
The y-intercept is = 90
Hence, the equation for the basketball line is:
y = 42x + 90
Equation for baseball:
We have the points:
(x1, y1) ==> (0, 150)
(x2, y2) ==> (5, 300)
Find the slope:
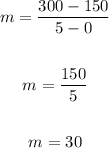
The slope of the baseballl line is 30
The y-intercept is 150.
Therefore, the equation of the baseball line is:
y = 30x + 150
• (3) To predict the salaries in the year 2000, we have:
2000 - 1980 = 20
This means the year 2000 is 20 years after 1980.
Substitute 20 for x in each equation and solve for y.
• Salary of basketball players in the year 2000:
y = 42x + 90
y = 42(20) + 90
y = 840 + 90
y = 930
The salary for basketball players in 2000 is $930 thousand.
• Salary of baseball in 2000:
y = 30x + 150
y = 30(20) + 150
y = 600 + 150
y = 750
The salary for baseball players in 2000 is $750 thousand.
ANSWER:
(1) the year where the salaries were equal is in 1985.
The estimated salary at year 5 was $300 thousand.
(2) Basketball equation: y = 42x + 90
Baseball equation: y = 30x + 150
(3) Basketball: $930,000
Baseball: $750,000