Question

from the base of the tower,you walk 36.37m.from there ,you use the clinometer to measure the angle of the incline from your eye to the top of the tower,and find that it is 75.you measure from the ground to your eye. the distance is 1.63mhow tall is the tower?(round the two decimal places if necessary)

Answer 1

An illustration of the given situation is shown below:

In order to determine the height x of the tower, take into account that the opposite side to angle 75° is (x - 1.63). Then, by using the tangent of 75°, you have:

`\tan 75=\frac{\text{opposite}}{\text{adjacent}}=(x-1.63)/(36.37)`

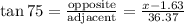
By solving for x and simplifying, you obtain:

`\begin{gathered} 36.37\cdot\tan 75=x-1.63 \\ x=36.37\cdot\tan 75+1.63 \\ x\approx137.36 \end{gathered}`

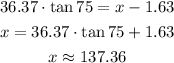
Hence, you can conclude that the height of the tower is approximately 137.36m