1 Answer

Ask a Question

Carlo · Answer 1 · 2023-04-26T19:07:55+0000

Answer:

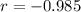
Explanation:

The Pearson correlation coefficient measures the strength of a linear association between two variables, where the value r=1 means a positive correlation and -1 a negative correlation.

It is represented by the equation:

$\begin{gathered} r=\frac{\Sigma(x_i-\bar{x})(y_i-\bar{y})}{\sqrt[]{\Sigma(x_i-\bar{x})^2}\sqrt[]{\Sigma(y_i-\bar{y)^2}}^{}} \\ \text{where,} \\ x_i=x\text{ values} \\ y_i=y\text{ values} \\ \bar{x}=\operatorname{mean}\text{ of x values} \\ \bar{y}=\operatorname{mean}\text{ of y values} \\ (x_i-\bar{x})(y_i-\bar{y})=\text{ deviation scores} \\ (x_i-\bar{x})^2\text{ and }(y_i-\bar{y)^2}=\text{ deviation squared} \end{gathered}$

Then, find all the corresponding values and operate to find the correlation coefficient:

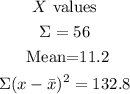
$\begin{gathered} X\text{ values} \\ \Sigma=56 \\ \text{ Mean=11.2} \\ \Sigma(x-\bar{x})^2=132.8 \end{gathered}$
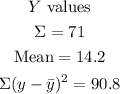
$\begin{gathered} Y\text{ values} \\ \Sigma=71 \\ \text{Mean}=14.2 \\ \Sigma(y-\bar{y})^2=90.8 \end{gathered}$
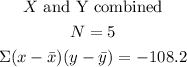
$\begin{gathered} X\text{ and Y combined} \\ N=5 \\ \Sigma(x-\bar{x})(y-\bar{y})=-108.2 \end{gathered}$

Now, using the formula for the coefficient:

$\begin{gathered} r=\frac{-108.2}{\sqrt[]{(132.8)(90.8)}} \\ r=-0.985 \end{gathered}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions