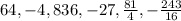Question

Write a rule for the nth term. Then graph the first six terms of the sequence.α3 = 36, r =34

Answer 1

Given:

`\begin{gathered} a3=36 \\ \\ r=-(3)/(4) \end{gathered}`

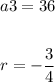
Required:

To find the rule for the nth term. Then graph the first six terms of the sequence.

Step-by-step explanation:

The nth term of the geometric sequence is given by

Here

`\begin{gathered} a_n=36 \\ n=3 \\ r=-(3)/(4) \end{gathered}`

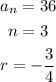
Now we have to find the value of a,

`\begin{gathered} 36=a(-(3)/(4))^(3-1) \\ \\ 36=a(-(3)/(4))^2 \\ \\ 36=a((9)/(16)) \\ \\ a=(576)/(9) \\ \\ a=64 \end{gathered}`

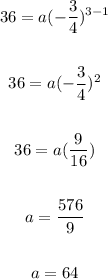
The first term is 64, therefore the formula is

`a_n=64(-(3)/(4))^(n-1)`

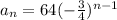
Now the first six terms of the sequence are

Therefore the first 6th terns are

`64,-48,36,-27,(81)/(4),-(243)/(16)`

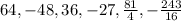
Final Answer:

The rule for the nth term is

`a_n=64(-(3)/(4))^(n-1)`

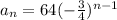
The first 6th terns are :

`64, -4,836, -27, (81)/(4), -(243)/(16)`