Solution:
Let x be the number of nickels and y be the number of dimes in Carolyn's purse.
There is $3.25 in her purse in nickes and dimes. T
Recall that;
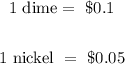
Thus;
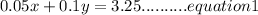
Also, the number of nickels is five less than three times the number of dimes. Thus;

Substitute equation2 in equation1;
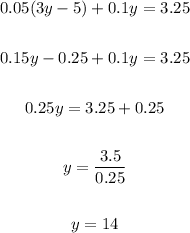
Substitute the value of y in equation2;
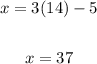
Hence, there are 37 nickels and 14 dimes in Carolyn's purse.