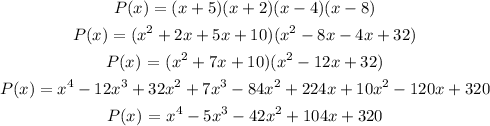ANSWER
The polynomial is:
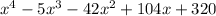
Step-by-step explanation
Note: If n is a zero of a polynomial, then (x-n) is a factor of the same polynomial. Hence, the factors for the given zeros are:
P(x) = (x+5)(x+2)(x-4)(x-8)
Let's multiply these out to obtain the polynomial in Standard Form.