Question

You run a spinner experiment with these results:bluecolorredgreenspins1110a. Find the experimental probability of spinning green .b. Find the experimental probability of spinning blue or greenc. What is the sample space for this experiment?

Answer 1

Total spins = 11 + 10 +9 = 30

Total spins of red = 11

Total spins of green = 10

Total spins of blue = 9

The formula for finding probability, P, is

`P=\frac{\text{required outcomes}}{possible\text{ outcomes}}`

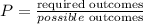
Let the probability of spinning a red be P(R)

Let the probability of spinning a green be P(G)

Let the probability of spinning a blue be P(B)

a) The experimental probability of spinning a green, P(R) is

`\begin{gathered} P=\frac{\text{required outcome}}{possible\text{ outcome}} \\ P(R)=\frac{\text{Total spins of green}}{Total\text{ spins}}=(10)/(30)=(1)/(3) \\ P(R)=(1)/(3) \end{gathered}`

Hence, the experimental probability of spinning a green is 1/3

b) The experimental probability of spinning a blue, P(B), is

`\begin{gathered} P=\frac{\text{required outcome}}{possible\text{ outcome}} \\ P(B)=\frac{\text{Total spins of green}}{Total\text{ spins}}=(9)/(30)=(3)/(10) \\ P(B)=(3)/(10) \end{gathered}`

The experimental probability of spinning a blue, P(B), is 3/10

The experimental probability of spinning a green, P(G), is 1/3

The experimental probability of spinning a blue or green, P(B OR G), will be

`\begin{gathered} P(B\text{ OR G)}=P(B)+P(G) \\ P(B\text{ OR G)}=(3)/(10)+(1)/(3)=(9+10)/(30)=(19)/(30) \\ P(B\text{ OR G)}=(19)/(30) \end{gathered}`

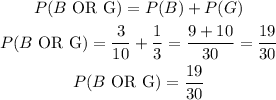
Hence, the experimental probability of spinning a blue or green, P(B OR G) is 19/30

c) The sample space for this experiment is the total possible outcome that can be obtained

Hence, the sample space for this experiment is 30