Question:
A rectangle's perimeter is 80 ft. Its length is 4 ft shorter than three times its width. Use an equation to find the rectangle's length and width.
Solution:
Let's denote by L the length of the rectangle, and by W its width. Now, if the length is 4 ft shorter than three times its width, we have the following diagram:
Then, we have the following equation:
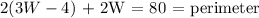
this is equivalent to:
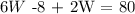
this is equivalent to:
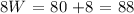
solving for W, we obtain:
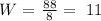
then, the width is 11 and the length would be:
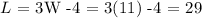
then, we can conclude that the correct answer is:
Length = 29
Width = 11