Question

Find the largest open interval where g(t) is increasingg(t)= -1/3 t^3+ 3/2t^2

Answer 1

Given the following function:

`g(t)=-(1)/(3)t^3+(3)/(2)t^2`

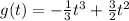
We will find the interval where g(t) incresing

The given function has a degree = 3 (odd number)

And has a leading coefficient = -1/3 (negative number)

So, as t tends to infinity the function g(t) tends to (∞)

the function will be decreasing on the both sides

And increasing in the middle

We need to find the local maximum and minumum points to find the inteval where g(t) increasing

We will graph the function g(t)

As shown the function has a local minimum at (0,0) and a local maximum at (3,4.5), between them the function increasing

So, the answer will be:

The interval of increasing = (0, 3)