The length of NO is 80.
Given:
The length of the side ML is 2x+50.
The length of the side NO is 4x+20.
The objective is to find the length of NO.
Since the given figure resembles the shape of a rhombus, the opposite sides are equal.
Then, the value of x can be calculated as,
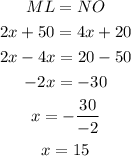
Now substitute the value of x in the equation of NO.
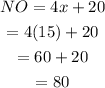
Hence, the length of NO is 80.