We have the next function
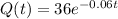
a)
For answer this section we need to find the value of Q when t=24

b)
In order to know how long will take until 1 gram of substance left we need to isolate t of the formula and Q=1
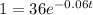
then we isolate t

c)
We have the initial amount that is when t=0
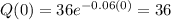
when t=10
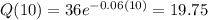
Then we calculate
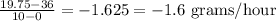
Because the result is negative it is decreasing