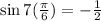Using the degree approach;
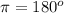
Then;
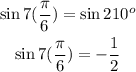
That is, the opposite is -1, and the hypotenuse is 2.
Also, following the image below;
Recall that;
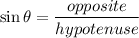
The opposite side is the side facing the angle, and the side facing angle 30 is -1. Then the third side is the adjacent.