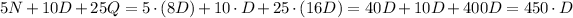Question

the amount of money in cents in a jar containing some nickels and (d) dimes and some quarters if there are 8 times as many nickels as dimes and twice as many quarters as nickels.the expression for the amount of money in the jar is ______ cents

Answer 1

The expression for the amount of money in the jar is 450d cents.

Step-by-step explanation:

The amount of money in cents in a jar can be determined by considering the values of nickels, dimes, and quarters in the jar. Let's denote the number of dimes as 'd'. Given that there are 8 times as many nickels as dimes, we can express the number of nickels as 8d. Additionally, the number of quarters is twice the number of nickels, which is 2(8d) = 16d.

The value of a nickel is 5 cents, so the total value of nickels is 5 * (8d) = 40d cents. Similarly, the value of a dime is 10 cents, so the total value of dimes is 10 * d = 10d cents. The value of a quarter is 25 cents, so the total value of quarters is 25 * (16d) = 400d cents.

To calculate the overall amount of money in the jar, we can add up the values of nickels, dimes, and quarters: 40d + 10d + 400d = 450d cents.

Therefore, the expression for the amount of money in the jar is 450d cents.

Answer 2

Let N be the number of nickels in the jar, D the number of dimes and Q the number of quarters in the jar.

Recall that a nickel is 5 cents, a dime is 10 cents and a quarter is 25 cents. So, the expression

`5\cdot N`

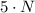
represents the total amount of cents we have, in nickels. In the same manner, we get the following expression for the dimes and the quarters

`10\cdot D`
`25\cdot Q`

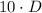
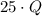
So, the total amount of cents we have in the jar would be the sum of these quantities. That is

`5N+10D+25Q`

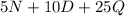
This is one valid expression. However, we would like to write an equivalent one using the information we are given.

First, we are told that there are 8 times as many nickels as dimes. This means that if we take the number of dimes D and multiply it by 8, we get the number of nickels N. That is

`N=8\cdot D`

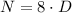
Also, we are told that we have twice as many quarters as nickels. That is that if we multiply by 2 the number of nickels, we get the number of quarters. So we have

`Q=2\cdot N`

Replacing the value of N that we found before, we have

`Q=2\cdot N=2\cdot(8\cdot D)=16D`

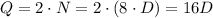
So now, we can replace all this values in our original expression. Thus, we end up with the expression

`5N+10D+25Q=5\cdot(8D)+10\cdot D+25\cdot(16D)=40D+10D+400D=450\cdot D`