ANSWER
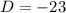
Two solutions that are imaginary
Step-by-step explanation
To find the discriminant, we apply the formula:
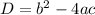
where a = coefficient of x², b = coefficient of x, c = constant.
From the given equation:
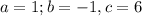
Therefore, the discriminant is:
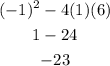
The given equation is a quadratic equation, hence, it will have two solutions but because the discriminant is less than 0, it will have two imaginary/complex solutions.