Question

$25,000 is invested, part at 11% and the rest at 10%. If the interest earned from the amount invested at 11% exceeds the interest earned from the amount invested at 10% by $242.60, how much is invested at each rate? (Round to two decimal places if necessary.

Answer 1

We have to find how much is invested at each rate.

We then can construct a system of 2 equations with 2 unknowns with the information given.

Let's call x to the amount invested at 11% and y the amount invested at 10%.

We know that the total amount invested is $25,000, so we have:

`x+y=25000`

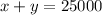
We also know that the interest earned from x exceeds the interest earned by y by $242.60.

The interest earned by x is equal to the interest rate times the amount, so it is 0.11*x.

The interest earned by y, in the same way, is equal to 0.10*y.

Then, we can write:

`0.11x=0.10y+242.60`

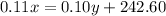
We can define y in function of x as:

`x+y=25000\longrightarrow y=25000-x`

and replace it in the second equation:

`\begin{gathered} 0.11x=0.10y+242.60 \\ 0.11x=0.10(25000-x)+242.60 \end{gathered}`

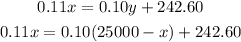
Then we can solve for x as:

`\begin{gathered} 0.11x=0.10(25000-x)+242.60 \\ 0.11x=0.10\cdot25000-0.10x+242.60 \\ 0.11x+0.10x=2500+242.60 \\ 0.21x=2742.60 \\ x=(2742.60)/(0.21) \\ x=13060 \end{gathered}`

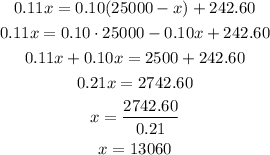
and y is:

`y=25000-x=25000-13060=11940`

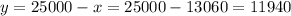
We can check the interest earned by the two investment as:

`\begin{gathered} I_x=0.11\cdot x=0.11\cdot13060=1436.6 \\ I_y=0.10\cdot y=0.10\cdot11940=1194 \\ I_x-I_y=1436.60-1194=242.60 \end{gathered}`

Answer:

There are $13,060 invested at 11% and $11,940 invested at 10%.