Question

Look at the steps and find the pattern.step 1step 2step 3How many dots are in the 28th step?dots

Answer 1

The Solution:

From the given picture,

Step 1 has 5 dots

Step 2 has 6 dots

Step 3 has 7 dots

Clearly, we can see that the sequence is a linear sequence.

By the formula for finding the nth term of an arithmetical Progression, which is

`T_n=a+(n-1)d`

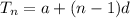
To find the number of dots in the 9th step, we shall use the above formula.

Where,

`\begin{gathered} d=\text{ number of dots in step2-number of dots in step1} \\ d=6-5=1 \\ a=5\text{ (number of dots in step1)} \\ n=28 \\ T_(28)=28th\text{ step} \end{gathered}`

Substituting these values in the formula above, we get

`\begin{gathered} T_(28)=5+(28-1)1 \\ =5+27 \\ =32\text{ dots} \end{gathered}`

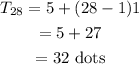
So, The 28th step has 32 dots.

Therefore, the correct answer is 32 dots.